El infinito matemático es contradictorio

 INFINITO, MATEMÁTICAS Y DIOS

El infinito matemático es contradictorio y lleva a aporías y paradojas

Resumen

Este estudio quiere ser una respuesta a  distintos artículos sobre el tema del infinito actual en matemáticas y también en las más recientes teorías de la física, recogidos en la revista Investigación y ciencia, serie Temas, nº 23, Ideas del infinito, del primer trimestre de 2003. Rechaza como filosóficamente indefendible el concepto de infinito actual, raíz de paradojas, incoherencias, inconsistencias lógicas en las matemáticas modernas, por ser contradictorio en sí mismo. Al hablar de infinito inevitablemente sale el tema del Ser Infinito, que las religiones llaman Dios y que en la filosofía aparece como el Ser Absoluto.

Sostiene que en el mundo de lo matemático sólo es coherente hablar  del llamado infinito potencial. Un infinito actual sólo lo puede ser un ser absolutamente simple, sin partes, no cuantitativo, que cae, por tanto, fuera del campo propio de las matemáticas: lo cuantitativo y medible.

Abstract

This study is a response to various articles on the subject of “actual infinity”  in mathematics and also in the latest physics theories, published in the journal Science and Research, Issues series, nº 23: Ideas of infinity, first quarter of 2003. It reject as philosophically untenable the concept of “actual infinity”, the root of paradoxes, logical inconsistencies in modern mathematics, for being self-contradictory.

It argues that in the mathematical world it is only coherent to talk about the socalled “potential infinity”. An actual infinity can only be an absolutely simple being, without parts, not quantitative and measurable. That absolutely simple being  is the God of Theology and religions, and the Absolute Being of Philosophy.

:::::::::::::::::::::::::

 

 El problema del infinito es ya muy viejo en la historia del pensamiento. Es más, algunos de sus problemas fundamentales, que hoy plantean matemáticos y físicos, ya los plantearon los griegos. Por ello, voy a recordar algunas de sus aportaciones, aunque sea de forma muy somera. Lo hago, además, porque algunos autores recientes parecen querer descubrir nuevos mediterráneos.

Anaximandro

Aunque la palabra “infinito” viene del latín infinitum, el concepto viene de los griegos. El primero en utilizar este concepto en cosmología fue Anaximandro de Mileto (siglo VI a.c.). De él sólo se conserva un texto en el que utiliza la palabra ápeiron[1] significando  materia primordial, ilimitada, indeterminada, incualificada, eterna, imperecedera (athánaton), incorruptible (athôlethron), inagotablemente fecunda, generadora de todos los seres. Es anterior a todas las determinaciones (concreciones de seres) y a todos los contrarios. Todas las cosas nacen de ella y todas retornan cíclicamente a ella.

De ese infinito originario nacen multitud mundos, esféricos, cerrados sobre sí mismos. Se originan de los remolinos formados por el movimiento eterno en el seno de ese infinito. Esos mundos nacen y se destruyen periódicamente, en ciclos fijos, pagando así la injusticia (desequilibrio) que se produce con su desprendimiento del infinito. Y es que toda la realidad está presidida por una ley cósmica necesaria que tiende a restablecer la igualdad entre los contrarios. Un especie de ley de Talión aplicada a la Naturaleza[2].

Espero que los físicos modernos del Universo no se ofendan si digo que algunas de sus teorías tienen importantes parecidos con esta de Anaximandro, salvando, por supuesto, las importantes diferencias en cuanto a fundamentación.

Cuando  S. Hawking y Mlodinow sostienen en Brevísima Historia del Tiempo que el Universo es autocontenido, insinuando o afirmando que la hipótesis de un Dios Creador no es necesaria para explicarlo, están sosteniendo como Anaximandro la eternidad de una materia primordial, que está más allá de todas las leyes de la física y que sin saber por qué sale de su estado caótico (sin ley) y entra en un proceso de diferenciaciones progresivas en las que aparecen toda clase de contrarios produciendo así los distintos sistemas estelares y galácticos, y también los del mundo cuántico.

El infinito de Anaximandro es interpretado por algunos especialistas como un ser divino (Dios), aunque de orden material. Pero decir que el Universo es autocontenido (completamente autosuficiente) y, por tanto, considerarlo como el origen último de todas las cosas no es menor divinización que la que hace Anaximandro. Por otra parte, el materialismo marxista tiene toda una teología de la Materia, como diosa metafísica, aunque material, de la que todo procede: eterna, omnipresente, omnipotente , creadora, omnisciente, etc. Un verdadero Dios[3].

La teoría de Anaximandro, con su visión circular y cíclica del devenir del Universo, adelanta ya una visión de expansión-retracción del mismo como apuntan algunas teorías modernas.

Aristóteles  [4]

Según Aristóteles, el tema del infinito es una cuestión ineludible para los físicos (entonces también filósofos y matemáticos). Después de aludir a cómo abordan el infinito los pitagóricos y Platón, sostiene que,

resulta evidente que el estudio y consideración del infinito

corresponde a los físicos (Aristóteles, 1973, 604).

Recordando la doctrina de sus predecesores en este tema, atribuye al infinito ciertas propiedades que tal vez convenga recordar, pues su olvido está en la raíz de algunos de los problemas que el tema del infinito está planteando a los matemáticos actuales. Dice Aristóteles:

No sin razón admiten todos que el infinito en sí es un principio; porque ni puede existir en vano ni poseer otra fuerza que la de un principio. Todas las cosas, en efecto, o bien son un principio o bien proceden de un principio; pero el infinito no tiene principio (origen), ya que, de lo contrario, tendría también término (fin). Además, es inengendrado y ajeno a la destrucción […] Por tanto, como decimos, no parece que el infinito pueda tener un principio, antes él es el principio de los demás seres y abarca y gobierna todas las cosas, como sostienen todos los que, fuera del infinito no admiten otras causas, como el espíritu o la amistad; el infinito, además, es un ser divino, ya que es inmortal y no puede perecer sin ser destruido, como afirma Anaximandro y otros muchos físicos (Aristóteles, o. c., 604).

Después de exponer ciertos argumentos a favor de la existencia del infinito y afirmar que “también las matemáticas emplean el infinito”, adelanta algo que está sucediendo actualmente con el tema del infinito:

Con todo, las consideraciones sobre el infinito encierran una dificultad, porque tanto los que rechazan su existencia como los que la admiten, se encuentran consecuentemente implicados en una serie inacabable de imposibles y absurdos (Aristóteles, o. c., 605).

Seguidamente ofrece dos sentidos en que se puede tomar el infinito. En un sentido, se llama infinito

lo que no puede ser trascendido ni excedido,

porque no es naturalmente apto para ser abarcado o medido (Aristóteles, o. c., 605).

Parece referirse al infinito actual, como luego veremos. Este tipo de infinito será el que posteriormente desarrollarán las teologías judía, cristiana y musulmana, considerándolo como un ser espiritual y absolutamente simple. De esa manera, elude todas las razones que más adelante desarrolla para rechazar el infinito actual de algunos matemáticos.

En otro sentido, infinito

es aquello cuya evolución no tiene término, o bien apenas lo tiene, o bien lo puede tener por su naturaleza, pero no lo tiene de hecho. Por lo demás, todo infinito lo es o bien por adicción, o bien por división, o bien de una y otra manera (Aristóteles, o. c., 605).

Parece referirse al infinito potencial, el único real para él, como enseguida veremos también.

Seguidamente dedica todo el capítulo 5 del Libro II de su Física para desarrollar sus argumentos en contra del infinito actual. El infinito actual que rechaza es un infinito de carácter cuantitativo, un infinito matemático, un infinito con partes y medible. Lo rechaza como un absurdo en sí mismo. Entiendo que su argumentación sigue siendo plenamente válida en nuestros días. La defensa, por otra parte, de un infinito así es la raíz de las paradojas e inconsistencias lógicas en el tratamiento que le dan las matemáticas modernas, sobre todo desde la teoría de conjuntos de Cantor.

Veamos las razones de Aristóteles para rechazarlo.

Así, pues, el infinito separado e independiente de los seres sensibles (como enseñan pitagóricos y platónicos),  un infinito que sea él mismo en sí un ser determinado, no puede existir, pues si el infinito en sí no es una magnitud ni una pluralidad, sino que es una sustancia y no un accidente, sin duda deberá ser un individuo. Pues lo que es divisible, será siempre una magnitud o una pluralidad (Aristóteles, o. c., 605).

Aristóteles está negando el infinito cuantitativo. Su razón fundamental es que tal infinito no es una realidad que exista por sí misma, sino una modalidad de la magnitud y del número. Es decir, es un accidente de otra cosa. No es sustancia que exista por sí misma. Por eso añade:

Por esta razón, hablan absurdamente los que afirman esto,

como son, por ejemplo, los pitagóricos, que admiten que el infinito es una sustancia

y, al mismo tiempo, lo dividen en partes (Aristóteles, o. c., 606).

Esta razón es precisamente la que más adelante desarrollo como la raíz principal de los errores de los matemáticos modernos, que defienden el infinito actual cuantitativo. Convierten en realidad actual independiente (sustancia, según Aristóteles) lo que sólo es una cualidad (modalidad) de las series numéricas  o conjuntos: la cualidad de ser aumentados indefinidamente, sin que podamos establecer  un límite último. Ser infinito actual y tener partes no es compatible, dice Aristóteles.

Para Aristóteles, un infinito cuantitativo

es evidente que no es posible que exista como algo dotado de existencia actual, ni como sustancia,
ni como principio,
pues de ser divisible, cualquier parte de él que se tomara sería también infinita,
porque la esencia del infinito es sustancia
y que la sustancia no se predica de ningún sujeto (Aristóteles, o. c., 606).

Es decir, un infinito divisible daría lugar a un número infinito de infinitos, lo cual es absurdo, pues unos limitarían (y, por tanto, negarían) a los otros. Aristóteles  entiende que un infinito actual sería un individuo que poseería una cantidad determinada y, por tanto, tendría partes. De ahí la razón de su argumento. De ahí también que concluya que la infinitud sólo se pueda entender como algo accidental de otra cosa, es decir, como una cualidad de otra cosa.

Es importante tener esto en cuenta para las críticas que le harán posteriormente los teólogos de fe bíblica. Aristóteles no niega un infinito espiritual y simple, sino un infinito cuantitativo actual. Se refiere a un supuesto infinito corporal (cuantitativo). Por eso dice:

Si la definición de cuerpo es aquello que está limitado por una superficie,
no puede existir un cuerpo infinito, ni inteligible ni sensible (Aristóteles, o.c., 606).

Luego añade una razón de por qué lo cuantitativo no puede ser infinito por concepto:

Ni siquiera el número, considerado como algo independiente o separado,
es infinito, porque el número, o lo que tiene un número,
es susceptible de ser contado (Aristóteles, o. c., 606).

Dicho de otra manera, nada que pueda ser numerado o medido es infinito. Cantidad e infinitud real son contradictorios, Si nos empañamos, como hacen muchos matemáticos modernos, en hacerlos compatibles, las paradojas, los absurdos, las incoherencias e inconsistencias lógicas serán inevitables.

Aristóteles, tras una larga argumentación concluye:

Por tanto, es evidente, según lo dicho,
que no existe en acto ningún cuerpo infinito (Aristóteles, o.c., 606).

Sin embargo, deja bien clara la existencia del infinito potencial, basada en el concepto de privación. Toda cantidad es susceptible de ser aumentada;  a cualquier serie de números se le puede añadir un número más; cualquier magnitud puede ser dividida más y más.  Y para consuelo de los matemáticos a quienes priva del infinito actual afirma:

                                                   Además, esta discusión de ninguna manera pretende privar a los matemáticos de sus consideraciones                                                               al eliminar la posibilidad de que el infinito exista de esta manera;
es decir, que exista en acto por adición o crecimiento,
como si no pudiera ser excedido o trascendido,
pues los matemáticos no precisan del infinito en sus estudios ni lo emplean en él,
sino que conciben la existencia de una magnitud finita
tan grande como quieran (Aristóteles, o. c., 611).

Los matemáticos modernos que defienden el infinito actual dan el salto de lo que consideran “muy grande”, con una magnitud que supera nuestra imaginación, al infinito actual. Ese salto es un salto en falso.

Para Aristóteles, el infinito, al contrario que en teología, es un signo de imperfección. La razón es que lo entiende como la posibilidad de adquirir un más  que todavía no se tiene. En palabras de Aristóteles, se trata del infinito entendido como causa material o potencial en sentido metafísico: posibilidad de ser lo que todavía no se es. Tiene, por eso, sentido de privación. Un infinito así entendido no es un sujeto o un individuo que exista por sí mismo. Es una propiedad de cosas que no existen por sí mismas. Es algo accidental. Por eso, concluye Aristóteles:

Es absurdo concebirlo como lo que comprehende o contiene
y no como lo que es contenido (Aristóteles, o. c., 611).

Concluyendo: Aristóteles afirma la existencia del infinito potencial como una propiedad de otra cosa, no como subsistente en sí mismo. Niega el infinito sensible  (cuantitativo) actual. No trata del infinito simple espiritual, que luego desarrollará la teología.

 

 

Concepto teológico de infinito

El desarrollo de este concepto empieza con Juan Pilopón (siglo VI), pero uno de los fiósofo-teólogos medievales que lo han tratado con más detalle fue Duns Escoto. En su Tratado del Primer Principio desarrolla ampliamente toda clase de razonamientos para demostrar por qué el Infinito en sentido estricto sólo puede ser uno y simple, y por qué una magnitud infinita (que  defienden muchos matemáticos modernos) es conceptualmente inviable o no es racionalmente sostenible; conduce a absurdos y contradicciones ya apuntados por Aristóteles. Sólo, como ejemplo, citaré un texto de Escoto. Enuncia su Décima Conclusión en los términos siguientes:

De la infinitud se sigue la simplicidad omnímoda,

y, entre otros muchos razonamientos da el siguiente:

Que (el infinito) no está compuesto de partes cuantitativas se prueba porque la perfección infinita no es una magnitud, porque aquella perfección, si es finita, sería más grande en una magnitud mayor; pero no puede haber una magnitud infinita. Este es el argumento de Aristóteles en el libro octavo de la Metafísica (D. Escoto, 1964, 104).

Considerar el infinito actual como una magnitud es precisamente el gran error de los matemáticos modernos que defienden la existencia del infinito actual cuantitativo y que les lleva a tantas aporías y contradicciones en su tratamiento del infinito.

 

Por otra parte, el infinito actual, desde un punto de vista meramente racional, lleva inexorablemente al Infinito con mayúscula. Lleva al Ser Absoluto, que las religiones denominan con múltiples nombres. Dicho de otra manera: no es racionalmente posible tratar el infinito actual sin entrar en teología, por más que le pese a algunos, que no quieren ni oír hablar de ella, así como tampoco de la metafísica. El infintio matemático es contradictorio y cargado de aporías y paradojas .http://Habló Stephen Hawking: la hipótesis de Dios no es necesaria. El Universso es autoconsistente

 

El infinito en las matemáticas actuales

El infinito matemático es contradictorio y lleva a aporías y paradojas.

Empecemos por el artículo de Javier de Lorenzo[5]. Hace una definición de los conceptos “infinito potencial” e “infinito actual”. En cuanto al concepto de infinito potencial no ofrece dificultades, pero sí en la del infinito actual.

Define el infinito potencial como un proceso de iteración o reiteración que jamás tiene fin, porque siempre hay un más allá.  Ej. La serie de números naturales; 1, 2, 3, 4, … Deja bien claro que el número natural está esencialmente ligado a la numeración y medida de magnitudes o cantidades de algo. Para medir algo se toma como unidad de medida una determinada cantidad de aquello mismo que se mide: el metro es una unidad de medida de la magnitud  de la extensión lineal (También se hace extensiva a la medida de superficies y de volúmenes, que son combinación de dimensiones lineales).

Quiero destacar esta idea de partida: los números naturales son magnitudes[6] y se emplean para medir. Por tanto, no se pueden aplicar a realidades no cuantitativas y que no sean medibles. Por otra parte, constituyen el punto de partida fundamental de las matemáticas.

La idea de infinito en matemáticas surge de la posibilidad de añadir a una determinada cantidad  “uno más” y esto de manera ilimitada. Es un concepto ligado a lo ilimitado.

También surge de la idea de aproximación sin fin hacia un límite previamente establecido. Por ejemplo:  2/3 o  raíz cuadrada de 2.  Es el infinito como convergencia asintótica hacia un límite. Es una cantidad que cada vez se acerca más hacia ese límite sin alcanzarlo nunca. Es un infinito entendido como un proceso de reiteración.

Por otra parte, está el infinito como producto. Aparece en los ejemplos de geometría. La superficie de los polígonos, tanto de los inscritos como de los circunscritos a un círculo, se aproxima indefinidamente hacia la superficie del círculo. El número de lados de esos polígonos siempre es un número natural concreto, y ese número tiende a infinito.  También se puede decir que la circunferencia se identifica en el límite con  un polígono de “infinitos lados infinitesimales”[7].

De Lorenzo afirma que este tipo de infinitos son ideales. Según él, la propiedad de infinitud es una propiedad métrica y la propiedad métrica la identifica como propiedad cuantitativa. Dice:

En el cálculo numérico, eso significa que el “uno más”, que caracteriza al infinito potencial, se presenta como propiedad métrica, cuantitativa; por cuya razón lo ilimitado sigue aquí identificado con el infinito potencial

Para clarificar esta afirmación de De Lorenzo hay que distinguir el “uno más” como posibilidad sin límite establecido y como acto real de numeración. Como simple posibilidad no se trata de una cuantidad medible, sino de una cualidad de ese tipo de cuantidad que es la serie numérica. Decir que se trata de una propiedad métrica y cuantitativa crea confusión.

Decir “uno más” es numerar, cuantificar. Pero vale para una cantidad finita cualquiera. Otra cosa es la de posibilidad misma de poder decir “uno más sin límite”. Esa posibilidad no es nada cuantitativo, nada que se pueda medir. Es anterior a toda medición y que hace posible la medición. Es una cualidad, que como tal cae fuera de todo cálculo o medición matemática. Es de carácter metafísico o metamatemático.

Un ejemplo claro nos lo ofrecen ciertos números irracionales como el número PI. Nunca dan un número exacto.  Siempre se puede añadir uno más. Esta es la irracionalidad de los números irracionales: nunca dan un cociente exacto ni periódico. Esa irracionalidad es una cualidad, no una cuantidad. Es una cualidad de una determinada cuantidad: la que se resiste a ser un número exacto. Esto lo expresó muy bien Euclides en la proposición 20 del libro IX de sus Elementos  que dice:

Hay más números primos que cualquier cantidad propuesta de números primos.

De aquí muchos matemáticos deducen que “el número de números primos es infinito”, identificando ilimitación con infinito actual. Pero eso, como dice de Lorenzo, ya puede ser un traición al sentido que le da Euclides. Se da un salto del infinito potencial al infinito actual, como si la contabilidad de “uno más” se hubiera llevado de hecho hasta el final, lo cual es contradictorio. Es negar la posibilidad misma del “uno más” de la que se partió.

En el cálculo infinitesimal  se vuelve a dar el mismo salto desde el infinito potencial al infinito actual, como apunta de Lorenzo[8]. Se da el salto  del infinito como proceso dinámico (un caminar sin límite hacia lo infinitamente pequeño) al infinito en acto: un conjunto con un número infinito de elementos infinitesimales considerados estáticamente.

De Lorenzo define así el concepto de infinito actual

 Es un infinito ilimitado, métrico, que permite la cuantificación y la resolución de problemas del mundo real (De Lorenzo, a. c., 8).

Es un infinito requerido por el propio proceso de cuantificación o numeración e incluye elementos ideales, como número infinito, punto infinito y series con infinitos elementos, dice De Lorenzo.

Pero decir “número infinito” es decir a la vez finito, porque es número, e infinito, lo cual es contradictorio. Lo mismo sucede cuando se dice “punto infinito”. Si digo “punto”, digo una realidad meramente ideal, sin dimensión alguna. Hablar de “punto infinito”, como hace De Lorenzo, no tiene sentido. Si se quiere decir un punto infinitamente pequeño, pero no igual a cero, será ya un elemento con dimensiones, por pequeñas que sean. Al utilizar la palabra “punto” se salta sin avisar de la noción geométrica originaria de punto (como elemento ideal sin dimensiones) a una realidad muy pequeña, pero que siempre tiene dimensiones.

Por otra parte, no le puedo aplicar la cuantidad de infinito. Una serie con “infinitos elementos” (infinitos puntos, por ejemplo) siempre será una serie con una cantidad determinada de elementos. No será nunca una cantidad infinita. Decir “cantidad” y decir “infinita” no son compatibles.

Un tercer camino para llegar al infinito actual es el del proceso de comparación biyectiva entre dos conjuntos  (más adelante expongo la teoría de Dedeking sobre la biyección entre conjuntos).  Ejemplo del pastor analfabeto, que no sabe contar, pero sí sabe cuál de dos rebaños es mayor que otro, comparando una a una las ovejas de un rebaño con las del otro. Ambos rebaños son conjuntos en acto y con un número finito de ovejas, aunque cada uno con la posibilidad de que se le pueda añadir siempre “una oveja más”, y esto sin límite: es el proceso ilimitado de la iteración como proceso “infinito”.

Se puede seguir comparando infinidad de pares de rebaños y aumentar en “uno más” el rebaño de cada par.

Se toma la serie de números naturales como ejemplo.  “Cada número se descompone de manera única en sus factores primos”, dice de Lorenzo, “así el conjunto de los números naturales es biyectivo con el conjunto de los números primos”. Es decir, tienen la misma extensión. Ambos son infinitos y tienen el mismo número cardinal. Siguiendo este razonamiento da como concepto de infinito el siguiente:

 

Un conjunto se dirá simplemente infinito si se puede poner en correspondencia biyectiva con una de sus partes. Así el conjunto de los números naturales es biyectivo con el conjunto de los números primos (De Lorenzo, a. c., 9).

 

Pone la biyectividad como demostración de la infinitud actual, que es de la que está tratando en el contexto. Pero la demostración no demuestra lo que pretende. La biyectividad se puede quedar, y así es, en la simple comparación de infinitos potenciales.

Para establecer la biyectividad, los conjuntos tienen que estar dados, dice. Pero quiero objetar que todo conjunto dado es siempre finito, por muy grande que sea. Y el hecho de que sea biyectivo con otro no demuestra en absoluto una infinitud actual. Al menos, si entendemos actual como dado de hecho o realmente y no meramente imaginario.

Anteriormente dice que el conjunto de números naturales es un infinito actual. No sé qué sentido puede tener esa infinitud, porque todo conjunto de números naturales dado será siempre un conjunto finito y siempre tendrá la posibilidad de ser aumentado (infinito potencial). Dicho de otra manera, todo conjunto de números naturales dado será siempre un conjunto finito en cuanto está realmente dado y será un infinito potencial porque siempre podrá ser aumentado. El conjunto de la totalidad de los números naturales nunca estará dado. Es un imposible metafísico. La que siempre estará dada es la potencialidad de aumentarlo “uno más”.

En el concepto de infinito que da en el texto citado anterior parece desconocer o, por lo menos, no tiene en cuenta la rica tradición que sobre ese concepto existe en la historia del pensamiento occidental. Es una definición que carece de rigor terminológico, porque deja la puerta abierta para confundir infinito con indefinido o con potencialmente ilimitado. En esa confusión conceptual radican muchas de las paradojas, si no todas, que se dan en las teorías matemáticas sobre el infinito.

De Lorenzo plantea también el problema de si hay uno sólo o varios infinitos. Toma la respuesta que da Cantor: Hay muchos infinitos y unos mayores que otros. Hay, por tanto, variedad de números cardinales, que simbolizan a esos infinitos.

Evidentemente, hay muchos infinitos, si por «infinito» se entiende una serie cuyo límite no está determinado y se puede aumentar indefinidamente.

El supuesto base del que parte es que los conjuntos tienen que estar dados, de lo contrario no se podrían comparar. Y saca esta consecuencia:

 Si un conjunto está dado, también lo están sus partes propias, es decir, el conjunto de todos los subconjuntos de dicho conjunto, lo que se denomina su conjunto potencia, cuyo cardinal es mayor que el correspondiente al del conjunto de partida (De Lorenzo, a. c., 9).

Aquí se dan dos pasos en falso. El primero consiste en afirmar que, si se da un conjunto, se dan sus subconjuntos potencia. La falsedad está en que si el conjunto de partida se da de forma concreta o real, no necesariamente se dan de la misma forma concreta sus conjuntos potenciales, tratándose de conjuntos meramente matemáticos. Puedo tener un conjunto de números naturales hasta 100 y no tener desarrollado el subconjunto de sus respectivas raíces cuadradas o el de sus respectivas potencias mil.

El segundo paso en falso consiste en sostener que el número cardinal del conjunto de los subconjuntos es mayor que el conjunto de partida.

En ambos casos se da un salto de lo potencial e ideal a lo actual. Se comparan dos entidades no comparables. No se puede decir que un conjunto meramente ideal o potencial es mayor o menor que otro real. Sería comparar dimensiones diferentes: la ideal y la real.

Es interesante a este respecto la observación que hace De Lorenzo:  En la naturaleza no hay infinito, ni potencial ni actual[9].  Y añade:

 Pero lo importante no es sustancializarlo como objeto, sino observar lo que subyace al mismo: las nociones mucho más primitivas de conjunto y de aplicación biyectiva de conjuntos (De Lorenzo, a. c., 9).

Sin embargo, más primitivas (originarias, diría yo) son las nociones de magnitud, cuantidad, número, cualidad, cuya confusión es la que crea problemas al hablar del infinito.

Por otra parte, si sustancializar el infinito no es lo importante, ¿en qué se queda el infinito actual matemático? Si no es nada concreto, ¿cómo se puede decir que es actual? ¿En qué consiste su actualidad o su entidad?

Seguidamente explica por qué es necesaria la idea de infinito y suponerlo como dado. Acude para ello al método de la diagonal. Y termina afirmando que el infinito es una conceptualización formal reguladora de la creación matemática. Pero, si es una simple conceptualización formal, ¿es algo actual o no lo es?  Por otra parte, queda la duda de si esa conceptualización está correctamente hecha o si está precisamente en la raíz de las paradojas e incongruencias que se siguen.

Concluye, no obstante:

Aunque haya de quedar bien entendido que  ningún matemático ha hecho, ni hará nunca, es una derivación ni un cómputo infinito (De Lorenzo, a. c., 9).

Y, si a esto añadimos que en la Naturaleza no existe ninguna cosa infinita, parece que hay que concluir que el infinito real  (actual), sea físico o matemático, no existe, aparte de que es conceptualmente un contrasentido, si se entiende como infinito actual cuantitativo.

 

EL PROBLEMA DEL INFINITO EN EL PROBLEMA DE LA CONTINUIDAD DEL MOVIMIENTO

Los problemas sobre la continuidad del movimiento, sobre su inicio y sobre su fin, los recoge  Michel Blay[10]. Se trata del viejo problema ya planteado por el griego Zenón y que Blay presenta en los siguientes términos:

Para alcanzar un punto dado, un móvil debe recorrer primero la mitad de la distancia que media hasta ese destino, después la mitad de la distancia restante y luego, la mitad de la distancia que falta; y así una y otra vez , indefinidamente. ¿Cómo recorrer una infinidad de mitades en un tiempo finito? (M. Baly, a. c., 18).

La paradoja planteada es falsa porque el problema está mal planteado. Veamos. La distancia a recorrer es finita. De antemano ya se ha establecido el punto de llegada. Luego se plantea el tema de la divisibilidad sin límite de esa distancia. Esa divisibilidad sin límite fijo es sólo un infinito potencial. Esa divisibilidad, desde el punto de vista físico, siempre será limitada. Otra cosa es que imaginariamente la podamos seguir  dividiendo.

En segundo lugar, el tiempo empleado en recorrer la distancia también es finito. Ese tiempo también lo podemos dividir sin límite en momentos cada vez más cortos. Esa división, desde  el punto de vista real, también tiene un límite, aunque imaginariamente podamos seguir dividiendo. Se trata de otro infinito potencial.

En ambos casos estamos ante realidades finitas que tienen la potencialidad de ser aumentadas indefinidamente, pero que en absoluto son infinitos reales o actuales.  La paradoja salta cuando del infinito potencial se da el salto a un supuesto infinito actual. Eso es lo que hace Blay cuando pregunta:

¿Cómo recorrer una infinidad de mitades en un tiempo finito?

En el texto antes citado utiliza la palabra “indefinidamente” para indicar la divisibilidad sin límite de la distancia a recorrer. Ahora, al plantear la paradoja, está suponiendo no una divisibilidad indefinida, sino infinita, es decir, un infinito actual. Da el salto del infinito potencial al infinito actual y ese salto es el que produce la paradoja.

Por otra parte, si la distancia a recorrer fuera realmente infinita (que no es el caso), también el tiempo para recorrerla sería infinito por la misma razón de su divisibilidad sin límite. La paradoja también en este supuesto imposible se queda sin fundamento.

Veamos cómo plantea Pascal el mismo problema, para luego hacer el comentario correspondiente. Dice Pascal:

Por raudo que sea un movimiento podemos concebir otro que lo sea más y apresurar aún más a este último; y siempre así, hasta el infinito, sin llegar jamás a uno que sea de tal suerte que nada le podamos añadir. Y al contrario, por lento que sea un movimiento, podemos todavía retardarlo más y lo mismo a este último; y así al infinito, sin jamás llegar a tal grado de lentitud que no se pueda descender todavía a una infinidad de otros, sin caer en el reposo (M. Blay, a. c., 18).

Blay resume el problema preguntando así:

¿Qué tratamiento matemático dar a las velocidades infinitamente pequeñas? ¿Cómo tratar matemáticamente velocidades infinitamente grandes?

Otra vez se da el salto de lo indefinidamente aumentable o disminuible al infinito actual. Lo que realmente tiene ante sí el matemático es una velocidad determinada y finita, una división finita, un aumento finito, una disminución finita. Son todas cantidades finitas, que tienen la posibilidad de ser aumentadas o disminuidas sin límite y  esa posibilidad nunca está agotada imaginariamente.

El problema que se plantea es el de la continuidad tanto del movimiento como del espacio y del tiempo, ya que el movimiento por excelencia es el local (espacial) y todo movimiento se mide por el tiempo. Se trata de saber si la velocidad del movimiento es divisible hasta el infinito, así como el espacio a recorrer y el tiempo empleado.

Los autores que tratan este problema, ya desde Zenón, pasando por  Cavalieri, Pascal, Galileo, etc. dan por supuesta esa divisibilidad hasta el infinito. Pero el concepto de infinito que manejan  no es el infinito actual, sino el potencial: la posibilidad de dividir límita la velocidad de un movimiento, o de dividir sin límite el espacio a recorrer o la duración (tiempo) que se tarda en recorrerlo.  Es un problema filosófico y también de la física moderna, que aún sigue sin resolver: una de los formas del problema del continuo.

En la astrofísica, por ejemplo, es el problema de si el vacío aparente entre los planetas y las galaxias está lleno de algo o está realmente vacío. Aristóteles ya postuló un quinto elemento: el éter, para llenar ese vacío. Con ese quinto elemento se completaba el cuarteto de elementos con el que se explicaba toda la materia: aire, agua, tierra y fuego.

La hipótesis del éter duró siglos. Finalmente, al no poder comprobar su existencia, fue desechada. Pero enseguida surgió la necesidad de rellenar ese vacío con otras hipótesis. Einstein lazó la suya, llamada constante cosmológica.Actualmente se recurre a las hipótesis de la energía oscura y la materia oscura.

El problema del continuo lo tenemos también en la biología de la evolución. Se plantea el problema del salto de una especie a otra más compleja. ¿Hay saltos creativos? ¿Hay continuidad? Si hay continuidad, ¿cómo se explica al paso de lo menos a lo más complejo? ¿Cómo se explica el paso de lo ontológicamente inferior a lo ontológicamente superior? Si la evolución va de lo menos a lo más, y si de la nada, nada se puede sacar (a no ser por un acto verdaderamente creador), ¿de dónde sale lo más que no estaba en lo menos? Al final, como siempre, nos topamos con un problema metafísico.

De la solución que se le dé dependen las modernas teorías de la física. Si digo que existen unos últimos elementos que ya no son divisibles, la divisibilidad hasta el infinito no se da y el problema del infinito desaparece: Estaríamos ante una visión atomista de la realidad, que en su esencia ya se remonta, al menos, hasta Demócrito.

Pero, si defiendo que los grados de la velocidad, los espacios a recorrer, las duraciones del tiempo empleado, se pueden dividir sin límite, entonces sí que surge el problema del infinito.

Blay recoge el planteamiento que hace Leibniz sobre el continuo en el movimiento. El planteamiento de Leibniz parece contradictorio. Me explico. Por un lado defiende el continuo en el movimiento. El movimiento no está entrecortado por pequeños reposos, como defienden los atomistas. Porque es continuo, es divisible hasta el infinito (infinito potencial). Pero no sólo eso. De hecho está dividido en infinitas partes. Esto equivale a defender el infinito actual.

Por otra parte, si está actualmente dividido en infinitas partes, cada una de esas partes es una especie de átomo, lo que Leibniz llama indivisibles. Y ahí está la posible contradicción de su teoría. Si hay indivisibles, que sumados constituyen un número infinito, entonces estamos negando el continuo y defendiendo de otra manera el atomismo.

Leibniz defiende la existencia de los indivisibles en el movimiento : el esfuerzo como un acto indivisible, que provoca el inicio del movimiento; el punto, como indivisible del espacio; y el instante, como indivisible del tiempo.

Para ver la incongruencia de su planteamiento basta con ver cómo trata el indivisible del espacio: el punto.  La noción de punto excluye toda dimensión. Es una noción puramente ideal; nunca puede llegar a ser real, porque toda realidad sensible, por pequeña que sea, es tridimensional[11].

Sin embargo, cuando Leibniz  (y actualmente muchos físicos y matemáticos) dice que  un espacio cualquiera consta de un número infinito de puntos, están suponiendo el punto como una especie de átomo, que sumado a otros, da lugar a una extensión determinada. Se da el salto de un punto meramente ideal a una visión física o material del punto.

Este confusionismo se observa una y otra vez  en las teorías atomistas actuales del espacio y del tiempo [12], así como en otras teorías como la de cuerdas, que no deja de ser una teoría atomista más.

El otro salto en falso que da Leibniz (que lo dan muchos físicos y matemáticos actuales en sus nuevas teorías) consiste en pasar del infinito potencial al infinito actual sin tener base empírica alguna para ello. Razonan así: Porque una extensión, un movimiento, una duración, una cantidad cualquiera, es divisible sin límite, se concluye que ya está infinitamente dividida de hecho.

Se rompe el principio clásico de la lógica: De posse ad ese non valet illatio, “del hecho de que una cosa sea posible no se sigue necesariamente que exista de hecho”. Del hecho de que un espacio lo podamos dividir más y más idealmente no se sigue que de hecho esté dividido infinitamente.

Además hay que tener en cuenta la siguiente limitación: Es un hecho insuperable el que nosotros, con todo el alcance de nuestros medios reales, no podemos dividir físicamente nada de manera indefinida, ni podemos aumentar nada de manera indefinida. Ni siquiera lo podemos hacer imaginativamente. Nuestra razón puede apuntar más allá de lo que podemos tanto física como imaginariamente, pero nunca podrá llegar al infinito real.

Aquí se plantea un problema de metafísica del conocimiento, que desarrollo en otras publicaciones. Su afirmación central es que el ser humano puede preguntar mucho más de lo que puede responder. Incluso puede preguntar por el Absoluto o el Infinito, con mayúscula. Sin embargo, es incapaz de dar una respuesta absoluta. Tal vez por eso, buscó esa respuesta absoluta en las revelaciones divinas que se suponen en muchas religiones; lo intentó en muchos sistemas filosóficos, y lo está intentando ahora en las modernas teorías de la Astrofísica y la Cosmología.

 

INFINITO GEOMÉTRICO 

Y  EL QUINTO POSTULADO DE EUCLIDES

Jean-Pierre Le Goff[13] recoge el 5º postulado de Euclides a propósito del tratamiento del infinito en geometría. Al  releer ese postulado me di cuenta de que la versión moderna del mismo no se corresponde exactamente con la versión original de Euclides. Por tanto, las otras geometrías no euclidianas, que supuestamente se desarrollan por oposición al quinto postulado de Euclides, en realidad se desarrollan por oposición a un postulado distinto al de Euclides.

La versión original del postulado dice que

si una secante corta dos rectas, formando ángulos internos situados a un mismo lado de la secante y cuya suma sea menor que dos rectos, las dos rectas, prolongadas indefinidamente (es decir, tanto como sea necesario), se cortarán en el mismo lado en que se encuentran los ángulos de suma menor que dos rectos.

Evidentemente, cuanto más pequeña sea la suma de esos dos ángulos, más cercano estará el punto de encuentro de esas dos rectas. Cuanto  más se acerque su suma a la de dos rectos, más lejano estará el punto de encuentro de las dos rectas. Y, si su suma fuera igual a la de dos rectos, hay que decir que las dos rectas son totalmente paralelas y no se cortarán nunca.

Seguidamente añade Le Goff la formulación moderna de este postulado, que dice ahora:

Dado un punto exterior a una recta en el plano, por él pasa una paralela a la recta y sólo una.

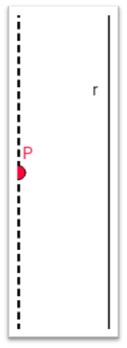
Esta versión no dice lo mismo que la original de Euclides, si se toma como concepto de recta el que aporta Desargues, como enseguida veremos. Según la versión de Euclides, las dos rectas no son paralelas. Si lo fueran, los dos ángulos a un mimo lado de la secante serían siempre igual a dos rectos. El hecho de que de uno de los lados su suma sea menor a dos rectos es prueba evidente de que de ese mismo lado las rectas tienden a juntarse a una distancia más o menos larga y, por tanto, no son paralelas. Una vez que se junten, constituirán un triángulo, del que un lado es la secante.

Un triángulo es un espacio cerrado en el que el infinito actual no tiene sentido, a no ser que lo identifiquemos con el infinito potencial: la posibilidad de alargar sus lados indefinidamente.

Por tanto,  tampoco es correcto  decir que, según Euclides, se juntan en el infinito, sino que tienden a juntarse en un punto más o menos lejano del punto de partida.

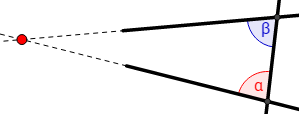
Si las geometrías no euclidianas modernas se quieren desarrollar por contraposición a la euclidiana, en realidad no es así. Lo hacen por contraposición a una derivación del postulado de Euclides.

En la fórmula de Euclides, el encuentro de las dos rectas no es una posibilidad  abierta o potencialidad. Ese encuentro ya está decidido por la amplitud de los ángulos con la secante.

En el caso de las paralelas, el encuentro ni siquiera es una posibilidad, si nos mantenemos en una geometría plana

De este falso supuesto parte Le Goff para poner el origen de las geometrías no euclidianas (la hiperbólica y la elíptica) en el desarrollo de la geometría prospectiva del siglo  XVII, enlazando ésta con la versión moderna del postulado euclidiano. Dice sobre su relación con la geometría euclidiana:

Fueron la invención de la perspectiva central y sus prolongaciones las que hicieron posible la irrupción y la consideración desapasionada en la geometría euclídea de elementos situados en el infinito (J-P. Le Goff, a. c., 30s).

Le Goff recoge los pasos dados por Desargues en geometría prospectiva. Desargues  asemeja dos rectas paralelas a dos rectas concurrentes, rompiendo así el paralelismo estricto, que es el verdaderamente euclidiano en su geometría plana.

Esto le lleva a decir que una recta no es más que un círculo de radio infinito; o lo que es  lo mismo, un círculo en el que una vez fijado uno de sus puntos, el centro se aleja del mismo indefinidamente; y que el cilindro no es más que un cono cuyo vértice se aleja también indefinidamente o se encuentra en el infinito.

Desargues, con este cambio que da al quinto postulado convirtiendo la recta en una curva, se sale de la geometría plana de Euclides y se mete en una geometría realista en la que no existe el espacio plano. El espacio en el que vivimos siempre es curvo. No se puede viajar a la Luna o a Júpiter en línea recta. No se puede trazar una línea recta euclidiana viajando sobre la superficie de la Tierra.

Sin embargo, Desargues no deja claro el concepto de infinito que maneja. Mas bien parece que lo identifica con lo indefinido, lo ilimitado; aquello cuyo límite no podemos establecer de manera definitiva. Esto se parece mucho más al infinito potencial que a un infinito actual. Se identifica la actualidad de la potencialidad con la actualidad de su realización.

Le Goff afirma que la geometría proyectiva que se desarrolla a partir de Desargues contribuye al desarrollo de las geometrías no euclidianas e incluso  a desarrollar modelos euclidianos para ellas.  El quinto postulado de Euclides en su lectura moderna: por un punto exterior a una recta pasa una sola paralela, es sustituido ahora por este otro: por un punto exterior a una recta pasan infinitas paralelas.

En realidad este nuevo principio se apoya en un nuevo concepto de recta, el establecido por Desargues, que poco tiene que ver con el concepto de Euclides[14] y que en realidad no es una recta, sino una curva que se cierra en un supuesto infinito, constituyendo un círculo.

Mi análisis de la figura (tomada del mismo artículo de  Le Goff): El texto a pie de imagen habla de “ramas infinitas” de la parábola, que se unen en un mismo punto cerrando así un espacio elíptico.  Habla también de un punto del infinito situado a distancia finita del observador.

Se utiliza el término “infinito” con una arbitrariedad que hace muy confuso todo el texto. Si dos parábolas se cierran formando una elipse, no se puede decir que son infinitas. Si un punto del infinito está a una distancia finita del observador no se le puede aplicar el calificativo de “infinito”.  La representación geométrica del infinito que se pretende resulta por sí misma contradictoria. Lo que aquí se califica de infinito es sólo un horizonte que está sujeto a la subjetividad de nuestra percepción de un punto lejano, que nada tiene que ver con un infinito actual.

Si me sitúo en el punto A y miro hacia el horizonte B, tengo la impresión de que todas las rectas, que en el punto A aparecen como paralelas, concurren en el punto B, dejando, por tanto de ser paralelas. Sin embargo, si me traslado al punto B, podré comprobar que las rectas siguen siendo tan paralelas como en el punto A. Si ahora desde el punto B miro hacia otro punto C situado en el horizonte lejano volveré a tener la impresión de que las rectas vuelven a ser concurrentes y dejan de ser paralelas.  Por tanto, la tesis de Desargues de que las paralelas son asimilables a rectas concurrentes y que una recta es una curva que se cierra en el infinito formando un círculo carece de todo fundamento.

No es una realidad, sino un problema de nuestra percepción. Una cosa es la impresión de perspectiva que yo recibo y la respresentación geométrica que hago de la misma, y otra cosa es la realidad objetiva. Esto se ve claro si observo objetos en el horizonte, que tienden a juntarse. Sin embargo, si me sitúo en el horizonte, se separan desmintiendo mi impresión anterior.

Concluyendo: El infinito geométrico se queda en un infinito potencial. Decir que la geometría proyectiva consigue una representación real del infinito actual no se sostiene. Toda representación geomzzzzzzzzzzzzzzzzétrica es por concepto una representación finita, por muchas proyecciones que se le quieran dar. Esas proyecciones son sólo flechas indicativas hacia un límite no determinado. Y eso es sólo un infinito potencial.

ANÁLISIS DE ALGUNAS PARADOJAS

DEL INFINITO ACTUAL EN MATEMÁTICAS

Las recoge en su artículo Jean-Paul Delahaye[15]. Éste pone en entredicho dos principios indiscutibles en la filosofía

tradicional: el de que el todo es mayor que cualquiera de sus partes y el de que la mente finita del ser humano es incapaz de concebir al infinito actual. El infinito actual en la teología de herencia bíblica (judía, cristiana y musulmana) sólo se puede predicar de Dios y es inseparable de la simplicidad absoluta; es decir, el infinito actual no puede, por concepto, tener partes. Un infinito actual constituido con partes es un absurdo. Ya lo dejó bien razonado D. Escoto.

Delahaye presenta la renuncia a esos dos principios como un acto de valentía, como una audacia, más que como un nuevo descubrimiento de la razón humana. Dice:

La reconsideración de este principio del todo y la parte se nos antoja de una audacia temeraria (subrayo) y por eso con frecuencia ha parecido preferible la conclusión de que solamente un ser infinito –Dios, por ejemplo- puede pensar lo infinito (J-P Delahaye, a. c., 38).

Y seguidamente añade:

Dos mil años serían necesarios para franquear este obstáculo. El principio del todo y la parte que, a decir verdad, apenas se usa en matemáticas, tenía que ser reconsiderado: este principio, eminentemente paradógico, impedía todo progreso hacia la comprensión del infinito actual. Tal audacia  (subrayo) será acometida por el filósofo y matemático checo Bernhard Bolzano.

Dice que el principio del todo y la parte es “eminentemente paradógico”.  Se refiere a las paradojas que surgen si se niega su validez, como sucede en el caso de los conjuntos infinitos actuales.  Para admitir su afirmación habrá que ver primero si los infinitos actuales son posibles o no. Mi conclusión será que no son posibles y que el principio euclidiano del todo y la parte sigue siendo tan válido como antes y, por supuesto, sin ninguna consecuencia paradójica.

La afirmación del infinito actual cuantitativo es en realidad la raíz de la negación del principio del todo y la parte. Es también la raíz de las demás paradojas. Veamos alguna de ellas y sus errores de planteamiento.

 

La paradoja del hotel infinito de Hilbert[16]

Esta paradoja se puede redactar como sigue:

Dos grandes hoteleros que querían construir el hotel más grande del mundo se reunieron a dialogar sobre el asunto y comenzaron por el primer y más obvio tema a discutir: cuántas habitaciones tendría.

—¿Qué te parece si construimos un hotel con 1000 habitaciones?
—No, porque si alguien construyera uno de 2000 habitaciones, nuestro hotel ya no sería tan grande. Mejor hagámoslo de 10.000.

—Pero podría ser que alguien construyera uno de 20 000 y volveríamos a quedarnos con un hotel pequeño. Construyamos un hotel con 1 000 000 de habitaciones, ése sería un hotel grande.

Como siempre podría llegar a haber un hotel más grande, llegaron a la conclusión de que era necesario hacer un hotel con habitaciones infinitas de manera que ningún otro hotel del mundo pudiera superar su tamaño.

Infinito más uno

Sin embargo, en un hotel de infinitas habitaciones no todo es camino de rosas. Tan pronto se abrieron las puertas de este hotel la gente comenzó a abarrotarlo y pronto se encontraron con que el hotel de habitaciones infinitas se encontraba lleno de infinitos huéspedes, lo cual es un inconveniente muy grave. En este momento surgió la primera paradoja, así que se tomó como medida que los huéspedes siempre tendrían habitación asegurada, pero con el acuerdo previo de que tendrían que cambiar de habitación cada vez que se les pidiera.

Fue entonces cuando llegó un hombre al hotel, pero este se encontraba lleno, por supuesto esto no preocupó al cliente pues en el Hotel Infinito se aseguraba que todos tendrían habitación. El hombre pidió su habitación y el recepcionista, consciente de que no habría ningún problema, tomó un micrófono por el que avisó a todos los huéspedes que por favor revisaran el número de su habitación, le sumaran uno y se cambiaran a ese número de habitación, de esta manera el nuevo huésped pudo dormir tranquilamente en la habitación número 1. Pero, ¿qué pasó entonces con el huésped que se encontraba en la última habitación? Sencillamente no hay última habitación.

Dos infinitos

Estando el hotel lleno de infinitos huéspedes, llegó un representante de una agencia de viajes su problema era que tenía una excursión de infinitos turistas que necesitarían hospedarse esa noche en el hotel. Se trataba, por lo tanto, de hacer sitio a infinitos huéspedes en un hotel con infinitas habitaciones, todas ellas ocupadas en aquellos momentos. Pero el recepcionista no tuvo ningún problema en aceptar a los nuevos turistas. Cogió el micrófono y pidió a todos los huéspedes que se mudaran a la habitación correspondiente al resultado de multiplicar por 2 el número de su habitación actual. De esa forma todos los huéspedes se mudaron a una habitación par, y todas las habitaciones impares quedaron libres. Como hay infinitos números impares, los infinitos turistas pudieron alojarse sin más problema, INFINITO × 2 = INFINITO

Infinito número de infinitos

Estando el hotel lleno con infinitos huéspedes, llegó otro representante de la agencia de viajes aún más preocupado que el primero y avisó al primero el gran problema que había ocurrido, ahora la agencia tenía un infinito número de excursiones con un infinito número de turistas cada una. «¡Qué enorme problema se presenta ahora!», pensaban los representantes de la agencia de viajes, ¿Cómo podrían hospedar a un número infinito de infinitos turistas? El recepcionista permaneció inmutable, por lo cual tomó tranquilamente el micrófono y se comunicó con todas las habitaciones y pidió que cada uno de los huéspedes multiplicara por dos el número de su habitación y se trasladaran allí.

Entonces asignó a cada una de las excursiones un número primo (distinto de 2) y a cada uno de los turistas de cada una de las excursiones un número par o impar (t), de manera que la habitación de cada uno de los turistas, se calculaba tomando el número primo de su excursión (p) y elevarlo al número que les tocó dentro de su excursión (t) lo que da: ��.

Existiendo un número infinito de números primos y un número infinito de números (pares e impares), fácilmente se logró hospedar a un número infinito de infinitos huéspedes dentro de un hotel que sólo tiene un número infinito de habitaciones.

A lo largo de todo el texto se confunde una y otra vez el infinito potencial y un su puesto infinito real. Hay tantos infinitos potenciales como cosas finitas que puedan se aumentadas. Por el contrario, el infinito actual, por concepto, sólo puede ser uno.

La paradoja es meramente ideal. Su error está en suponer que el hotel tiene realmente un número infinito (actual) de habitaciones y que cada autocar trae un número infinito actual de viajeros, cuando en realidad sólo se trata de números finitos, que tienen la posibilidad  o potencialidad meramente ideal (no real) de ser aumentados indefinidamente. Esa posibilidad de aumento indefinido no es una cantidad concreta, que pueda ser medida o tratada matemáticamente. Es sólo una cualidad de esos números concretos: número de habitaciones, número de viajeros y número de autocares. Es su condición de posibilidad, que es anterior a toda medida o cálculo matemático.

Así que, puesto que el infinito actual no se da, tampoco se da la paradoja. Es una aparente o falsa paradoja. Aristóteles sigue teniendo razón cuando niega toda existencia física al infinito actual.

El todo es mayor que cada una de sus partes: Euclides

La relación todo-parte es sólo una posibilidad que puedo desarrollar o dejar en mera posibilidad o potencialidad. Como tal potencialidad,  no es una cantidad de nada, sino una cualidad de cada uno de esos números. Y es que los números, aunque miden cantidades, también tienen cualidades  que no son medibles o numerables.  Se trata de la dimensión metafísica de los números, que no suele ser tenida en cuenta por los matemáticos y que está en la raíz de tantas aporías e inconsistencias lógicas en el tratamiento del infinito matemático.

El  principio de que el todo es mayor que cada una de sus partes es siempre verdad en el orden de las cosas reales físicas y también en el orden de las cantidades numéricas concretas. En el orden de las cantidades numéricas concretas (finitas), cualquiera de ellas puede ser mayor que otra, independientemente de que, si comparo dos de ellas, una sea considerada parte de la otra o un todo que contenga a la otra. Esa independencia es un valor que indica la no aplicabilidad a la relación entre ambas del principio de que el todo es mayor que cada una de sus partes.

Una  serie concreta de los números naturales puede ser mayor o menor que una serie concreta de los cuadrados correspondientes. La serie de números naturales puedo extenderla y terminarla en el 100, por ejemplo. La serie de los cuadrados puedo terminarla en 121, por ejemplo, como una serie totalmente independiente, aunque cumpla la relación de que cada uno de sus miembros es el cuadrado de un miembro de  la serie primera. Lo mismo que puedo considerar que cada miembro de la serie primera es la raíz cuadrada de cada uno de los miembros de la segunda serie.

Por otra parte, cualquiera de los cuadrados está ya presente en la serie de números naturales como un número natural más: el 4, el 9, el 16, etc., están en la serie misma de los números naturales. Esta propiedad: la de que un mismo número sea número natural y a la vez sea el cuadrado de otro número natural, no es reversible entre la serie de números naturales y la serie de sus respectivos cuadrados, pues no todos los números naturales son, a su vez, el cuadrado de otro número natural. Por tanto, habrá siempre más números naturales que números que tengan la propiedad de ser cuadrados de un número natural. Esta propiedad muestra que la serie de números naturales es siempre mayor que la de sus respectivos cuadrados, si hacemos terminar una y otra serie en el mismo número.

Por otra parte, cada número natural no sólo es raíz cuadrada de su cuadrado, sino que, a la vez, tiene su propia raíz cuadrada, que puede ser un número exacto (limitado) o un número inexacto (ilimitado). Cada raíz cuadrada tiene a su vez su propia raíz cuadrada, y esto sin límite. Esto sucede con cualquiera de las otras raíces matemáticas.

El infinito potencial aparece por todas partes. Es una cualidad del universo de lo cuantitativo. Como tal cualidad es pre-matemática. Es una condición de posibilidad del universo matemático. Y como tal condición previa no  puede ser objeto del cálculo matemático. Es de orden metafísico, objeto de la filosofía de los números.

Se trata de una cualidad, que podemos llamar asintoticidad, y de la que no se puede decir que sea mayor o menor en una serie o conjunto que en otro. Sin embargo, sí se puede decir que es igual  en unos y en otros, contra lo que apuntaba Galileo y posteriormente Cantor. La asintoticidad es una cualidad que es independiente de que un conjunto se tome como parte de otro o como un todo. Puede atribuirse por igual a uno y a otro. Esta igualdad en la asintoticidad del infinito potencial es la que confunde a los matemáticos, como Bolzano, que quiere sacar del universo de las matemáticas el principio de Euclides: el todo es mayor que cada una de sus partes. Por el contrario, en cuanto a la cantidad, el conjunto de números naturales siempre será mayor que  el de los números pares o el de los impares, etc.

El principio del todo y la parte hay que considerarlo como una limitación de la lógica humana mas bien que como un principio paradógico, como dice Delahaye. Es algo parecido al principio de indeterminación establecido por Heisenberg como otra limitación infranqueable del conocimiento humano en el universo cuántico.

Por otra parte, en cuanto a lo que dice Delahaye sobre la afirmación filosófico-teológica de que sólo Dios es capaz de pensar el infinito (actual, se supone) es un obstáculo (para el progreso de las matemáticas, se sobreentiende), tengo que decir  que se equivoca. Sigue siendo válida la afirmación filosófico-teológica de que el ser finito no puede abarcar con su pensamiento el infinito actual. Sólo un ser infinito (llámese Dios o como se quiera) puede hacerlo. Sólo Él es, por otra parte, el infinito actual, capaz de pensarse a sí mismo[17]. Hasta aí lo que puede dar de sí nuestra razón.

Cuando el ser humano quiere pensar el infinito actual, tropieza irremisiblemente con el misterio. Es decir, se encuentra con la puerta cerrada. Si persiste en penetrar en él, entonces vienen las paradojas y las inconsistencias lógicas.

La aversión que ciertos matemáticos (y también físicos) muestran hacia la teología y también hacia la metafísica es difícil de justificar, como no sea por su desconocimiento de ambas. En cualquier caso, por más que quieran, no se pueden librar de ellas, como se ve en sus propias teorías. Cuando la expulsan por la puerta principal, se les cuela por la puerta trasera en forma de supuestos  en los que se apoyan sin analizarlos o someterlos a reflexión. Se podrían poner muchos ejemplos.

 

 Bolzano contra Euclides[18]

Delahaye recoge el planteamiento que hace Bolzano contra el principio euclidiano de que el todo es mayor que las partes. Bolzano quiere resolver la paradoja de la reflexividad entre conjuntos. Para ello propone que se debe distinguir entre el concepto de “estar contenido en” y el concepto de “tener menor tamaño que”. Según Bolzano, el que un conjunto (la parte) esté contenido en otro (el todo) no conlleva el que el conjunto-parte tenga menor tamaño que el conjunto-todo.  Ambos pueden tener el mismo tamaño (llamado también cardinal). Esto viola el principio euclidiano de que el todo es siempre mayor que la parte.

Bolzano, para negar el principio euclidiano, se basa en la correspondencia biyectiva entre los miembros de una serie (la de los números naturales, por ejemplo) tomada como un todo y una de sus partes (la serie de los cuadrados respectivos de cada número natural de esa serie-todo).

(NB: Confunde un a vez más la igualdad del infinito potencial (cualidad) entre ambos conjuntos con la supuesta igualdad de su supuesta infinitud actual).

Este planteamiento de Bolzano se oscurece, si bajamos al mundo de los conjuntos reales. Pongamos un conjunto de dos naranjas y otro de cuatro. El de cuatro puede ser considerado como el cuadrado del de dos. Sin embargo, son dos conjuntos diferentes, de tamaño diferente.

Pero Bolzano se apoya en el infinito actual que propone Leibniz en su doctrina sobre el Universo:

Estoy tan a favor del infinito actual que, en lugar de admitir que la naturaleza lo aborrece, entiendo que la afecta por completo, para mejor resaltar la perfección de su Autor (En Delahaye, a. c., 38).

El infinito actual de Leibniz se refiere al número infinito de mónadas que constituye el Universo como totalidad. Pero a la vez rechaza la divisibilidad hasta el infinito, porque rechaza el concepto de materia como extensión  de Descartes. La materia se constituye en último término de elementos puramente dinámicos: las mónadas. Son pura fuerza, simples, inextensas, indivisibles, inmateriales, ingeneradas e incorruptibles; cada una de ellas es única e irrepetible; cerrada sobre sí misma, sin ventanas o apertura alguna hacia las demás, es decir, son incomunicables entre sí[19].

Dicho de otra manera: Según Leibniz, la materia se compone en último término de elementos inmateriales o espirituales, puramente dinámicos. Su número es un infinito actual:

Cada porción de materia no sólo es divisible hasta el infinito, sino que está ya dividida actualmente hasta el fin (Leibniz, 1972, nº. 65).

No obstante, el infinito actual de Leibniz no es equiparable al infinito actual de los matemáticos. Para compararlos habría que resolver previamente el problema leibniziono de cómo de seres simples, inextensos  (lo que equivale a decir “espirituales”) pueden salir seres extensos materiales en el sentido corriente de “material”. ¿O es que la extensión es mera ilusión de nuestros sentidos? Recurrir a Leibniz como un argumento de autoridad a favor del infinito actual matemático no ofrece mucha garantía. No es lo mismo sumar cantidades extensas o cuantitativas que entidades simples, no cuantitativas, como son las mónadas o átomos de Leibniz, cada una de las cuales es única, porque tiene sus propias cualidades. Los matemáticos hablan de cuantidades repetibles sin fin, que tienen muy poco qué ver con las mónadas leibnizianas. Así que no es lo mismo decir infinito actual en sentido leibniziano que infinito actual en sentido de los matemáticos modernos.

De hecho, para Delahaye, es Bolzano el primero en defender el infinito actual matemático en su obra Paradojas de lo infinito (1851), publicada tras su muerte. Según Bolzano, los números cuadrados están contenidos en el conjunto de los enteros, pero una y otra totalidades tienen el mismo tamaño (o sea, el mismo número cardinal)[20].

El argumento dice que si el conjunto de los cuadrados es un infinito actual, que tiene el mismo tamaño (número cardinal) que el infinito actual  de los naturales, el principio de que el todo es mayor que la parte queda invalidado.

(Se confunde la igualdad del infinito potencial con una supuesta igualdad de un supuesto infinito actual. Es decir, se aplica al infinito actual la infinitud propia del infinito potencial). 

Sin embargo, en el mundo físico no es posible que el contenido tenga el mismo tamaño que el continente. Dificultades de esta solución:

1ª- Ambos conjuntos no tienen el mismo tamaño: En el conjunto de números naturales hay números que no están en el de los cuadrados:  2, 3, 5, 7  no son cuadrados de ningún otro número natural. La biyectividad entre ambos conjuntos sólo es parcial.

2ª- La igualdad de tamaño a que se refiere Delahaye parece ser  la igualdad en la infinitud  de ambos conjuntos. Pero esa igualdad ya no es una igualdad cuantitativa actual, sino  una igualdad en cuanto a la potencialidad que tienen ambos conjuntos de ser ampliados indefinidamente. Esa potencialidad no es una cantidad concreta a la que se pueda atribuir un tamaño determinado. Esa potencialidad es una cualidad de ambos conjuntos, que no es en absoluto incompatible con el hecho de que uno de ellos sea el todo y el otro una de sus partes.

3ª- Hay que tener en cuenta que todos los cuadrados, los cubos, y demás potencias de los números naturales ya están contenidos en la serie misma de los números naturales: El 4, lo puedo considerar como un número natural simple o como el cuadrado de 2; el 8 lo puedo considerar como un número natural simple o como el cubo del número 2. Y así sucesivamente. Pero la serie de números naturales tiene números que no son cuadrados de otros ni son cubos de otros, etc. Esto demuestra que el conjunto de números naturales siempre será mayor que cualquiera de sus subconjuntos, cuando sus cantidades estén determinadas.

Dondequiera que pare la serie de cuadrados, su última cifra siempre estará también en la de números naturales. Por el contrario, la de números naturales tiene cifras que no estarán nunca en la de los cuadrados. La biyectividad no se cumple.

Cada número natural es el punto de partida de una serie de conjuntos de potencialidad ilimitada. A partir del 3 se pueden ir sacando raíces de raíces indefinidamente, lo mismo que cuadrados de cuadrados o cubos de cubos (potencias de potencias), etc.

Sorprende lo que dice Delahaye para resolver el problema:

Es necesario aceptar (subrayo) lo que parecía paradógico y decretar (subrayo) que la paradoja desaparece por un desdoblamiento conceptual: “estar contenido en” no implica “tener menor tamaño que” (Delahaye, a. c., 39) .

“Aceptar” y “decretar” son dos actos de la voluntad. Esos actos sólo son necesarios si lo que se acepta y decreta se muestra como evidente, ya sea por intuición directa o por demostración.  La intuición directa no se da en este caso; más bien se da la intuición directa de todo lo contrario, es decir, la intuición del principio de Euclides.

Sólo queda, entonces, que esa necesidad venga de una demostración incontrovertible. Si ésta no se diera, los actos de aceptar y decretar anteriores serán dos actos libres de la voluntad. En este caso, la arbitrariedad estaría en la base misma del panteamiento de Bolzano, que luego continuará Cantor, como veremos más adelante.

Delahaye cita al alemán  Georg Cantor  como el gran autor que desarrolla el álgebra de las biyecciones entre conjuntos, que no desarrolló Bolzano, y como la gran autoridad que defiende los infinitos actuales.

 

La respuesta de R. Dedeking

Define el infinito diciendo que un conjunto es infinito, si se puede establecer una correspondencia biyectiva entre cada uno de sus miembros y los de  un subconjunto, que es parte suya. La definición es confusa. No aclara si se trata de un infinito potencial o actual, aunque por el contexto parece referirse al actual.  Por otra parte, supone el mismo error de Bolzano. Delahaye dice que ésta es la definición de conjunto infinito que se utiliza actualmente en la teoría de conjuntos. Habrá que tenerla en cuanta más adelante.

 

La solución de G. Cantor

De Cantor se dice que ha convertido la teoría de conjuntos en la teoría en la que se fundan todas las matemáticas modernas. Esta fue la razón por la que la teoría de conjuntos se ha convertido en la forma más habitual de enseñar las matemáticas.

 

Es una afirmación fundamental de Cantor el que los conjuntos infinitos pueden tener una infinidad de tamaños diferentes. Se basa para ello en la no correspondencia biyectiva entre el conjunto tomado como un todo originario y sus subconjuntos.  El lenguaje utilizado es muy confuso una vez más.

En primer lugar, decir “conjunto” es ya decir una cantidad determinada y, por tanto, finita. Añadir que es “infinito”, si se entiende como infinito actual, es contradictorio, y más si se habla de muchos conjuntos infinitos.

En segundo lugar,  decir que distintos infinitos tienen distintos tamaños también es contradictorio. No se puede hablar de “tamaño” sin pensar en una cantidad determinada y, por tanto, finita. Sólo se puede hablar de tamaños diferentes entre cantidades finitas. Lo contrario es violentar tanto el lenguaje  que se vuelve demasiado confuso, si no incomprensible.

En tercer lugar, Cantor hace una distinción entre infinito numerable e infinito no numerable. Se basa para ello en el método de la diagonal[21]. Se aclara que el infinito numerable es aquel conjunto en el que podemos enumerar todos sus elementos. Ahora bien, decir “infinito numerable” es un contrasentido. Si podemos enumerar todos sus elementos es a todas luces un conjunto finito, aunque tenga la potencialidad de ser aumentado sin límite. Una vez más, la infinitud en matemáticas sólo se puede entender como infinitud potencial.

A pesar de todo, Delahaye atribuye un “resultado asombroso” a las investigaciones de Cantor al respecto. Según Cantor, el conjunto de puntos de una superficie (de un cuadrado, por ejemplo) es de igual tamaño que el conjunto de puntos de un segmento de una recta. Una recta y un plano (incluso un espacio de dimensión  n) son idénticos desde el punto de vista del tamaño de su infinitud.

En primer lugar, Cantor sigue tomando el infinito potencial como un infinito actual, cosa que no parece sostenible por las razones que aporto.

En segundo lugar, Cantor parece suponer que el punto tiene dimensiones, cuando, por concepto, no las tiene, a no ser que cambiemos el concepto. Aquí subyace el gran problema del continuo y el problema de la división indefinida de toda dimensión: sea una línea, una superficie o un volumen[22]. Esa división indefinida siempre tendrá un límite físico, más allá del cual el hombre no tendrá capacidad físico-técnica para seguir dividiendo, aunque lo pueda seguir haciendo imaginariamente.

Según dice Delahaye,

Cantor demostró que el conjunto P(N) de las partes de un conjunto N es siempre estrictamente mayor que el conjunto N. De aquí se sigue la existencia de una infinidad de conjuntos cada vez más grandes. N, P(N), P(P(N))) y, accesoriamente, que no existe el conjunto de todos los conjuntos (Delahaye, a.c., 44).

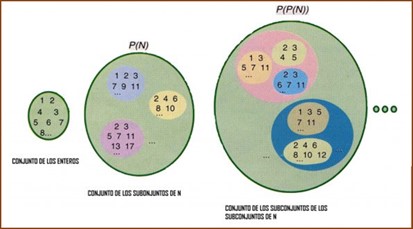
En la ilustración que pone Delahaye se hace evidente el fallo de la teoría de Cantor. Pone un círculo representando el conjunto N de los números naturales: 1, 2, 3, 4, 5, 6, 7, 8 … Luego pone en un círculo mayor, el subconjunto P(N) de supuestas partes del conjunto N y lo pone como un círculo mayor que el que representa al conjunto de los números enteros. Dentro de ese subconjunto pone como partes  del conjunto N los siguientes grupos: 1, 2, 3, 7, 9, 11, …; 2, 4, 6, 8, 10, …; 2, 3, 5, 7, 11, 13, 17.

En un segundo subconjunto P(P(N)), como subconjunto de P(N), pone los siguientes grupos como partes del subconjunto P(N): Un grupo que abarca los siguientes subgrupos: 1, 3, 5, 7, 11, …; 2, 3, 4, 5, …; y 2, 3, 6, 7, 11, … Y otro grupo que abarca los subgrupos: 1, 3, 5, 7, 11, … y 2, 4, 6, 8, 10, 12, … Y representa ese nuevo conjunto de partes del conjunto N con un círculo aún mayor que los conjuntos N y P(N), a pesar de que sólo recoge algunas partes (algunas combinaciones de las muchas que son posibles) de los dos conjuntos  anteriores..

Cantor parte del supuesto de que cada conjunto o grupo son infinitos actuales. La tesis de cantor consiste en afirmar que el subconjunto P(N), a pesar de que es sólo una parte del conjunto N, es, sin embargo, mayor que N. El subconjunto P(P(N)), a pesar de que sólo es una parte de P(N), es, sin embargo, mayor en tamaño que P(N) y mucho mayor que N.

En realidad, si el conjunto N sólo recoge las partes  1,2,3,4,5,6,7,8, y el conjunto P(N) añade las partes 9, 10, 11, 13 y 17, éste P(N) es realmente mayor que N. Lo mismo sucede con el conjunto P(P(N)), porque añade partes nuevas a las de los conjuntos anteriores. Vistos así los tres conjuntos, no hay paradoja ninguna.

Pero, si el conjunto N lo tomo como un todo ilimitado («infinito») y los conjuntos P(N) y P(P(N)) los tomo también como ilimitados o infinitos en sentido cantoriano, entonces da la im presión de que un conjunto con varios infinitos es mayor que un solo conjunto infinito. Y así surge la paradoja.

La paradoja está en que, según esta teoría, el todo N es menor en tamaño que el conjunto de sus partes. Esto va contra el principio o noción común de Euclides: “El todo es mayor que la parte”, un principio que parece evidente e innegable.

En mi análisis de la teoría de Cantor, éste comete un error, que es raíz de  paradojas y de conclusiones lógicamente insatisfactorias en el manejo de la noción de infinito en la teoría de conjuntos y en general en las matemáticas.

Las combinaciones de números naturales que se hacen en el subconjunto P(N) no son partes actuales o reales del conjunto N, como se supone en la teoría. Son meras potencialidades en el conjunto N. Como ya indiqué más arriba, las potencialidades de un número no son un número o cantidad, como se supone en la deducción de Cantor. Son una cualidad. Las cualidades no tienen tamaño. No son realidades cuantificables.

El conjunto P(N) tal como se recoge en la ilustración de Delahaye y en la teoría de Cantor no es un subconjunto de N como se supone. Tampoco el conjunto P(P(N)) es un subconjunto de P(N). Se trata sencillamente de conjuntos distintos, cada uno de los cuales tiene su propia potencialidad de ser extendido indefinidamente. Como cantidades concretas, son siempre conjuntos finitos. Como tales, son unos mayores que otros. Y la magnitud de cada uno no está establecida a priori. Depende de hasta qué límite se contabilice en cada uno. Ese límite real o actual se establece siempre a posteriori. Según esto, cualquier conjunto con potencialidad ilimitada puede ser mayor o menor que otro.

Mantener la idea de parte actual en los subconjuntos anteriores está en la raíz de posteriores aporías e incongruencias, y la supuesta invalidación del principio de Euclides antes aludido.  Si yo quisiera traducir  a cosas los conjuntos anteriores ( a conjuntos de granos de trigo, por ejemplo), quedaría muy claro que se trata de conjuntos distintos e independientes entre los que no se da la relación todo-parte. Esa relación de conjunto, subconjunto, subconjunto del subconjunto, etc.,  tal como la presenta Delahaye en su ejemplo, no la puedo aplicar a cosas concretas sin que me salgan conjuntos diferentes e independientes unos de otros. Cabe, entonces, la pregunta de si esas relaciones, meramente ideales, estarán correctamente establecidas.

Siendo así las cosas, se entiende mejor lo que dice Cantor: Un conjunto N no puede ser nunca puesto en correspondencia (biyección) biunívoca con el conjunto de sus partes, que se denota P(N)[23]. Pero la razón de esa no correspondencia no es la que apunta Cantor. La razón es mucho más sencilla: esos conjuntos considerados como partes no son verdaderas partes de N. Son sencillamente nuevos conjuntos. Si digo que son subconjuntos de N, ya los declaro como partes de N, establezco la relación todo-parte y siento las bases de todas la paradojas que lógicamente se siguen después.

Si corregimos ese paso en falso que se da desde un conjunto original a una serie de subconjuntos derivados, las paradojas o contradicciones (antinomias) y las insatisfacciones lógicas desparecen. La afirmación de Gauss (1777-1855) a este respecto se comprende entonces sin dificultad:

Me opongo a que se utilice un objeto infinito como un todo completo; tal operación está prohibida en matemáticas; el infinito no es más que una forma de hablar( En Delahaye, a. c., 38).

Por otra parte, aún suponiendo que todos los subconjuntos P(N) , P[P(N)], sean partes de N, habría que decir que están en la potencialidad de N y nunca superan su potencialidad. N, en este sentido, siempre tendría todas las pontencialidades de cada una de sus partes, más otras pontencialidades que cada una de ellas por separado no tiene. El todo, por tanto, sigue siendo mayor que cada una de sus partes.

En cualquier caso, hay que distinguir cuándo se trata de conjuntos distintos al originario y cuándo de verdaderos subconjuntos del originario.

Entiendo, además, que la forma más prudente de definir un número primo (un infinito potencial en general) sigue siendo la que dio Euclides:

Los números primos son más grande cantidad que toda cantidad de números primos propuesta.

De esta manera no nos salimos del universo de lo cuantitativo y, por tanto, numerable o matematizable. Introducir infinitos actuales ha traído muchos más problemas que los que ha resuelto.  Por otra parte, como afirman los constructivistas, muchos de esos problemas se pueden resolver  por la vía constructiva sin recurrir a los infinitos actuales. Ese tipo de infinitos sigue siendo tan absurdo como lo era antes de Cantor y de las teorías que han intentado resolver las paradojas que producen.

No hay problema en hablar de infinitos matemáticos mayores y menores siempre que esos infinitos se entiendan en sentido cuantitativo, que es el verdadero sentido matemático de los mismos.  Esos infinitos sólo pueden tener la cualidad de la infinitud, si ésta se entiende en sentido asintótico o potencial, cuya magnitud concreta suponemos indeterminada. Y entre finitos cuantitativos y potenciales, por muy grandes que los imaginemos, siempre es posible hablar de mayor y menor. Como se dijo anteriormente, la infinitud se toma no como cantidad, sino como cualidad: la cualidad de la asintoticidad. Si la tomamos como cantidad, caemos en el infinito cuantitativo actual, que es conceptualmente insostenible.

La asintoticidad o infinitud potencial se atribuye por igual a todos los infinitos cuantitativos, que en realidad son finitos. Tratarlos como si fueran infinitos cuantitativos (que lo son) y a la vez actuales es la raíz de todos los confusionismos posteriores. Todos los problemas y aporías surgen de identificar la cualidad de la asintoticidad o infinitud potencial con un infinito cuantitativo actual, que es en sí mismo un concepto contradictorio.

El que una serie tenga la capacidad de ser extendida sin límite en dirección a una meta o límite que no podemos determinar es una cualidad de esa serie. Es una cualidad que hace que esa serie sea distinta de otras. Su carácter distinto no viene determinado por la cantidad que tenga en cualquier momento del proceso de su extensión. Esa cantidad siempre es una cantidad finita que no se distinguiría de otra cantidad finita de la misma magnitud, aunque ésta segunda no fuera asintótica o no tuviera la posibilidad de ser ampliada indefinidamente. La posibilidad de ser ampliada indefinidamente no es una cantidad, es una cualidad.

Por otra parte, vendría bien para aclarar esta cuestión tener en cuenta el reciente artículo de Agustín Rayo sobre la naturaleza de los números[24].  De las tres principales opciones sobre la naturaleza de los números: la platónica, la consecuencialista y el platonismo moderado, opta por éste. Según el platonismo moderado, la expresión numérica del mundo físico es sólo una de las expresiones que se pueden hacer; los números no tienen entidad propia; son sólo una forma de expresión del mundo físico.

Y  yo concluyo que, si es evidente que en el mundo físico no existen infinitos actuales, tampoco existen, por tanto, en el universo de los números.

Por todo lo expuesto, la conclusión a que llega Delahaye en su artículo citado queda invalidada. Dice Delahaye refiriéndose a que las contradicciones o paradojas producidas por la admisión del infinito actual han sido superadas:

Pero pudieron ser eludidas en el plazo de pocos años (…) y lo que a algunos pareció el fracaso de la teoría matemática del infinito (actual) proporcionaría, en definitiva, la ocasión para que esta teoría se forjase una armadura que nada ha podido rasguñar seriamente hasta el día de hoy (Delahaye, a. c., 41).

Entiendo que esa armadura se ha roto y que nunca ha tenido la consistencia que sus defensores le atribuyeron. Prueba de ello es esta afirmación del mismo  Delahaye al final de su artículo:

Podemos incluso pensar que las situaciones lógicamente insatisfactorias que todavía creemos percibir se irán disipando a medida que nuestro entendimiento vaya aceptando (subrayo) plenamente el nuevo universo conceptual propuesto por estas matemáticas del infinito actual (Delahaye, a. c., 44).

En este texto parece que toda la seguridad mostrada en el texto anterior se difumina y la duda se deja ver amenazadora. Y es que también se puede pensar todo lo contrario de lo que espera Delahaye.

Da la impresión de que se trata de aceptar algo que va contra nuestro sentido común o contra nuestra propia razón; o de aceptar algo como si se tratara de un postulado, cuando, por otra parte, no se presenta como un postulado, sino como una teoría bien armada.

Para terminar, creo que es oportuna la observación que el gran físico y matemático Ernesto Sábato nos hace respecto a los límites de las matemáticas, límites que estaría bien tener en cuenta en toda esta problemática sobre el infinito. Dice Sábato:

Frente a la infinita riqueza del mundo material, los fundadores de la ciencia positiva seleccionaron (subrayo) los atributos cuantificables: la masa, el peso, la forma geométrica, la posición, la velocidad. Y llegaron al convencimiento de que <<la naturaleza está escrita en caracteres matemáticos>>, cuando lo que estaba escrito en caracteres matemáticos no es la naturaleza, sino… la estructura matemática de la naturaleza. Perogrullada tan ingeniosa como la de afirmar que el esqueleto de los animales tiene siempre caracteres esqueléticos (E. Sabato, 1988, 36). 

Tengo la impresion de que el infinito matemático funciona como una especie de escondite, que está a oscuras, donde cada matemático juega a lo que más le gusta y con la ventaja de que siempre gana, porque en esa oscuridad nadie le puede rebatir. La fantasía vuela sin control, a pesar de tener algunas coincidencias con la realidad, que sirven de apoyo y excusa al matemático del infinito, para seguir fantaseando. Algo muy similar es lo que está sucediendo en los últimos tiempos con las teorías de la Física. Surgen teorías y contrateorías casi a diario, para explicar el origen del Universo, ciertos fenómenos cuánticos o la armonización de la mecánica cuántica con la teoría einstiniana de la relatividad así como otros muchos problemas, teorías que van más allá de lo que  al método estrictamente científico permite[25].

:::::::::::::::::::::::::::::::::::

CONCLUSIONES

Entiendo que habría que retornar a ciertos viejos principios en los que la filosofía y las matemáticas se funden la una en la otra. Los que aquí interesan para el tema que tenemos entre manos se pueden resumir en este silogismo:

Todo lo que tiene partes es finito.

Todo lo cuantitativo tiene partes.

Todo lo cuantitativo es finito.

A esto habría que añadir a la ya muy vieja y muy discutida noción de infinito en el sentido más estricto de la palabra: Sólo un ser simple (sin partes) puede ser infinito actual.

Ese tipo de infinito cae fuera de las matemáticas por no ser cuantitativo. Las matemáticas, por concepto, sólo se aplican a realidades cuantitativas, medibles, y que, por tanto, tienen partes. La matemática es, por esencia, número y todo número es una cantidad.

El infinito cuantitativo actual no existe, porque es contradictorio en sí mismo, y lo es porque al tener partes, es finito. Esto ya lo intuyó e intentó demostrar Aristóteles y fue ampliamente discutido en la flosofía y teología de la Edad Media y Moderna.

El infinito actual sólo puede ser un ser simple, sin partes, sin principio ni fin, ni en el espacio ni en el tiempo. Es, por tanto, un ente ilimitado en su ser y en el tiempo; es eterno. Es el Dios de las religiones y de la teología. Es también el Ser Absoluto de la filosofía. Aquí no se aborda el problema de si un tal ser existe realmente o no. Eso sólo es cuestión de fe o creencia. Cada uno puede creer que existe o que no existe. Tan creencia es lo uno como lo otro. El ateo más radical es también un creyente: no cree que ese Ser Absoluto o Dios exista en realidad.

 

REFLEXIÓN FINAL

El problema del infinito parece un problema inevitable para la mente humana. Esta ya lo plantea, en uno u otro sentido, incluso en sus mitos más antiguos. Es un problema ampliamente discutido en filosofía, en teología,  en matemáticas y también en la física.

Está íntimamente ligado a otras cuestiones fundamentales cómo cuál es el origen del universo, si es eterno o no; si fue creado y existe un Creador (Dios); si es ilimitado (infinito) o si tiene frontera (límite); si existe el continuo y en qué consiste; si es ilimitadamente divisible o se dan los indivisibles (átomos o partículas) como realidades últimas, etc.

En cuanto a las respuestas que se han ido dando hay que tener en cuenta ciertos mitos en torno al tiempo, que parecen determinantes en el tipo de respuesta: se trata de los mitos del Gran Tiempo, que desarrollo en otra publicación[26].

Una visión circular y cíclica del tiempo, como la tuvieron los griegos, tal vez tomada del hinduismo, parece propicia para entender el infinito en sentido esférico. Para los griegos, la esfera era el símbolo de lo perfecto y también de lo ilimitado. En la esfera no hay un inicio ni un término o fin. Para Aristóteles, el Universo es esférico y con un movimiento circular eterno, un movimiento de rotación, que es, para él, el  movimiento perfecto, sin un punto de partida ni un punto de llegada. Se trata de un infinito cerrado y, por tanto, físicamente finito.

El infinito abierto, el infinito potencial, es un principio de imperfección, para él. Es un principio de lo que puede ser, pero que todavía no  es. Tiene un sentido de privación y, por tanto, apunta hacia perfecciones que faltan o que todavía no se tienen, aunque se puedan llegar a tener.

No quiero terminar este trabajo sin añadir lo que creo un error de algunos matemáticos modernos. Estas matemáticas, desde que se transfiguraron en su versión más formalista y abstracta, se separaron de la realidad física, se convirtieron en operaciones meramente formales y autoconsistentes.  Muchos matemáticos, en lugar de seguir utilizándolas como instrumentos de medida de la reladad física, les dieron entidad autónoma y las convirtieron  en una ciencia independiente con un fin en sí misma.

Sin embargo, no hay que olvidar que el origen de los números  está en la necesidad que tiene el hombre de medir las cosas de su vida cotidiana. En ese mundo no hay infinitos actuales. Sólo hay  conjuntos de cosas, que pueden ser aumentados o disminuidos por adición o sustracción, como ya decía Aristóteles; o que pueden ser divididas hasta cierto límite.

Cuando el matemático se olvida de ese origen práctico de los números y empieza a hacer operaciones abstractas con ellos, y, sobre todo, cuando renuncia totalmente a la religación de las matemáticas con la realidad física, y se marcha a un mundo totalmente formalista y platónico, es entonces cuando empiezan a surgir los problemas del infinito. La realidad física debiera ser siempre su punto de referencia irrenunciable. Querer sustancializar  las matemáticas, declarándolas autosuficientes y con valor por sí mismas, es cortarles los pies y dejarlas sin fundamento. No debieran olvidar nunca su carácter instrumental: medios para medir cosas distintas a ellas mismas. Ahí está su fuerza y su limitación más radical.

BIBLIOGRAFÍA

 ARISTÓTELES. 1973. Obras. Madrid: Aguilar.

 BLAY, Michel. 2001. “La ciencia del movimiento en el siglo XVII”.  Investigación y Ciencia, serie Temas, nº. 23: 18-22.

 DIELS, Hermann. 1985. Vorsokratiker, I. Zürich-Hildesheim: Weidmann.

 ESCOTO, J. Duns. 1964. Tratado del Primer Principio. Buenos Aires: Aguilar Argentina S. A. de Ediciones.

 DELAHAYE, Jean-Paul. 2001. “El carácter paradójico del infinito”.  Investigación y Ciencia, serie Temas.  nº. 23, 36-44.

DE LA PIENDA, Jesús Avelino. 1992: El Panteón de los dioses marxistas, I –II. Oviedo: Servicio de Publicaciones de la Universidad de Oviedo.

 -2006. Los mitos del Gran Tiempo. Madrid. BIBLIOTECA NUEVA

 -2008. El baile de la ciencia y la metafísica. Madrid: BIBLIOTECA NUEVA.

 DE LORENZO, Javier 2001. “El infinito matemático”.  Investigación y Ciencia, serie Temas, nº. 23: 4-9.

 EUCLIDES. 1991.  Elementos, Libro I. Madrid: Gredos.

 FRAILE, Guillermo, 1960. Historia de la Filosofía. Vol. I. Madrid: BAC.

 LE GOFF, Jean-Pierre. 2001.  “La perspectiva y el infinito matemático”.  Investigación y Ciencia, serie Temas, nº. 23: 30-35

 LEIBNIZ. 1972. Monadología. Buenos Aires: Aguilar Argentina S. A. de Ediciones.

 PUERTAS, Mª. Luisa. 1991. Euclides. Elementos. Libro I. Madrid: Gredos

 RAYO, Agustín. Junio 2009: “Juegos matemáticos”.  Investigación y Ciencia. pp. 90-91.

 SÁBATO, Ernesto. 1988. Hombres y engranajes. Heterodoxia. Madrid: Alianza Editorial.

 SMOLIN, Lee. 2006. “Átomos del espacio y del tiempo”.  Investigacióny Ciencia, serie Temas, nº. 43: 68-76.

::::::::::::::::::::::::::::::::::::::::::::::

NOTAS

[1] Puede verse el texto griego en H. Diels: Vorsokratiker, I, Weidmann, Zürich-Hildesheim, 1985, p. 89.

[2] Cfr. Guillermo Fraile: Historia de la Filosofía.. Vol. I: Grecia y Roma, BAC, Madrid, 1960, pp. 108-112.

[3] Cfr. J. Avelino de la Pienda: El Panteón de los dioses marxistas, I –II, Universidad de Oviedo.

[4] Aristóteles toca este tema en varios de sus textos, pero principalmente en su Física, Cap. 4-7, y en Del Cielo, Cap. 6-7. Utilizaré la versión castellana de Ediciones Aguilar: Aristóteles. Obras, Madrid, 1973.

[5]  Javier de Lorenzo. 2001. “El infinito matemático”, Invesitigación y Ciencia. Serie Temas, nº.23: 4-9.

[6] Creo, no obstante, que sería más exacto decir que son símbolos que sirven para medir y expresar magnitudes. Los símbolos no son magnitudes: no medimos el 4, sino que utilizamos el símbolo 4 para medir cosas. Evidentemente puedo medir el tamaño del símbolo  4 cuando está escrito, pero entonces ya no mido el 4 en cuanto símbolo, sino en cuanto realidad física.

[7]  Cfr. De Lorenzo. a. c.,  5.

[8]  Idem.  a. c.,  6.

[9] Cf. Idem, a. c., p. 9.

[10]  Michel Blay “La ciencia del movimiento en el siglo XVII”. Investigación y Ciencia, serie Temas, nº 23: 18-22.

[11]  Según Euclides en Elementos, “el punto es lo que no tiene partes”.  Esta definición es la que domina en la tradición filosófica y geométrica posterior. Pero lo que no tiene partes es simple y no tiene dimensiones: Si las tuviera, ya sería algo divisible en partes. Por eso Leibniz llama indivisibles, simples (mónadas, término pitagosico), a las realidades últimas. Pero después describe la mónada como un reflejo o microcosmos del macrocosmos, lo cual parece difícilmente compaginable con la simplicidad de la mónada.

[12] Cf. Lee Smolin. 2006. “Átomos del espacio y del tiempo”. Investigacióny Ciencia, serie Temas, nº 43: 68-76.

[13] Jean-Pierre Le Goff: “La perspectiva y el infinito matemático”.  Investigación y Ciencia, serie Temas, nº 23: 30-35.

[14]  Euclides, en la definición 4 de Los elementos,  define la recta como  aquella línea “que yace por igual respecto de los puntos que están en ella”. Esta definición no está exenta  de dificultades conceptuales. Por ello, la definición de recta que ha tenido más éxito es la de Arquímedes, que dice: “La recta es la más corta de todas las líneas  que tienen los mismos extremos” (Cfr. Euclides. 1991. Elementos, Libro I. Madrid: Gredos (Boblioteca Clásica de Gredos), p. 190, nota 2 de Mª. Luisa Puertas.

[15]  Jean-Paul Delahaye. 2001. “El carácter paradójico del infinito”.  Investigación y Ciencia, serie Temas, nº 23: 36-44.

[16]  La descripción de la paradoja puede verla el lector en el citado artículo de Delahaye.

[17]  Es éste un tema ampliamente discutido y desarrollado por la filosofía teológica, que no procede recoger a quí.

[18]  Recogida en su obra póstuma Paradojas del infinito, publicada en 1851, después de su muerte.

[19]  Me sorprende comprobar que la fórmula E=mv² ya la había establecido Leibniz: la fuerza o energía, dice Leibniz, es igual a la masa por la velocidad al cuadrado. Para entender el sentido que le da Leibniz hay que tener en cuenta su metafísica de la materia y las mónadas (cfr. G. Fraile. 1978. Historia de la Filosofía, III,  669). La meteria es, para él, esencialmente energía, afirmación que tiene mucho que ver con la mecánica cuántica actual.

[20]  Delahaye, a. c.,  39.

[21]  Idem, a., c., 40, recuadro c y p. 41, comentario al recuadro.

[22] Sobre la problemática del concepto de punto puede verse Mª. Luisa Puertas en Euclides. Elementos,.1991. Madrid: Edit. Gredos. Libro Primero, nota 1, pp. 189s.

[23]  Cfr. Delahaye, a. c., 39.

[24]  Agustín Rayo. Junio 2009.  “Juegos matemáticos”.  Investigación y Ciencia, serie Temas, nº 23, pp.  90-91.

[25]  Véase J. A. de la Pienda. 2008. El baile de la ciencia y la metafísica. Madrid: Edit BIBLIOTECA NUEVA.

[26]  Véase J. Avelino de la Pienda. 2006. Los mitos del Gran Tiempo. Una filosofía del tiempo. Madrid: Edit.l BIBLIOTECA NUEVA.